The basic X-Wing strategy is based on two Rows with constraints on two Columns, or vice-versa. In the Franken X-Wing strategy, we use a Column and a Square with constraints on two Rows (or a Row and a Square with constraints on two Columns).

CBRR Franken X-Wing

If a particular Candidate is present in only Two Cells in a Column,
if you can find a Square that does not overlap this Column and where the Candidate is present in the same two Rows as in this Column,
then these Cells form a pattern called an CBRR Franken X-Wing (derived from the BB/CC Franken X-Wing). Such a pattern allows eliminating the Candidate from all Cells in the Rows of the CBRR Franken X-Wing except from the Cells that are included in the CBRR Franken X-Wing itself.

If the Candidate is the solution in the first Cell of the Column, then it must be the solution in the second Row of the Square; if it is the solution in the second Cell of the Column, then it must be the solution in the first Row of the Square. Hence, whichever the solution for the Candidate in the Column, it can not be the solution in any Cell of the involved Rows outside of the CBRR Franken X-Wing.

The candidate must not be present in all Cells of the Square of the CBRR Franken X-Wing, as long as it is present in at leat one Cell of the involved Rows.

The reasoning is also applicable when you replace "Column" by "Row" and "Row" by "Column".

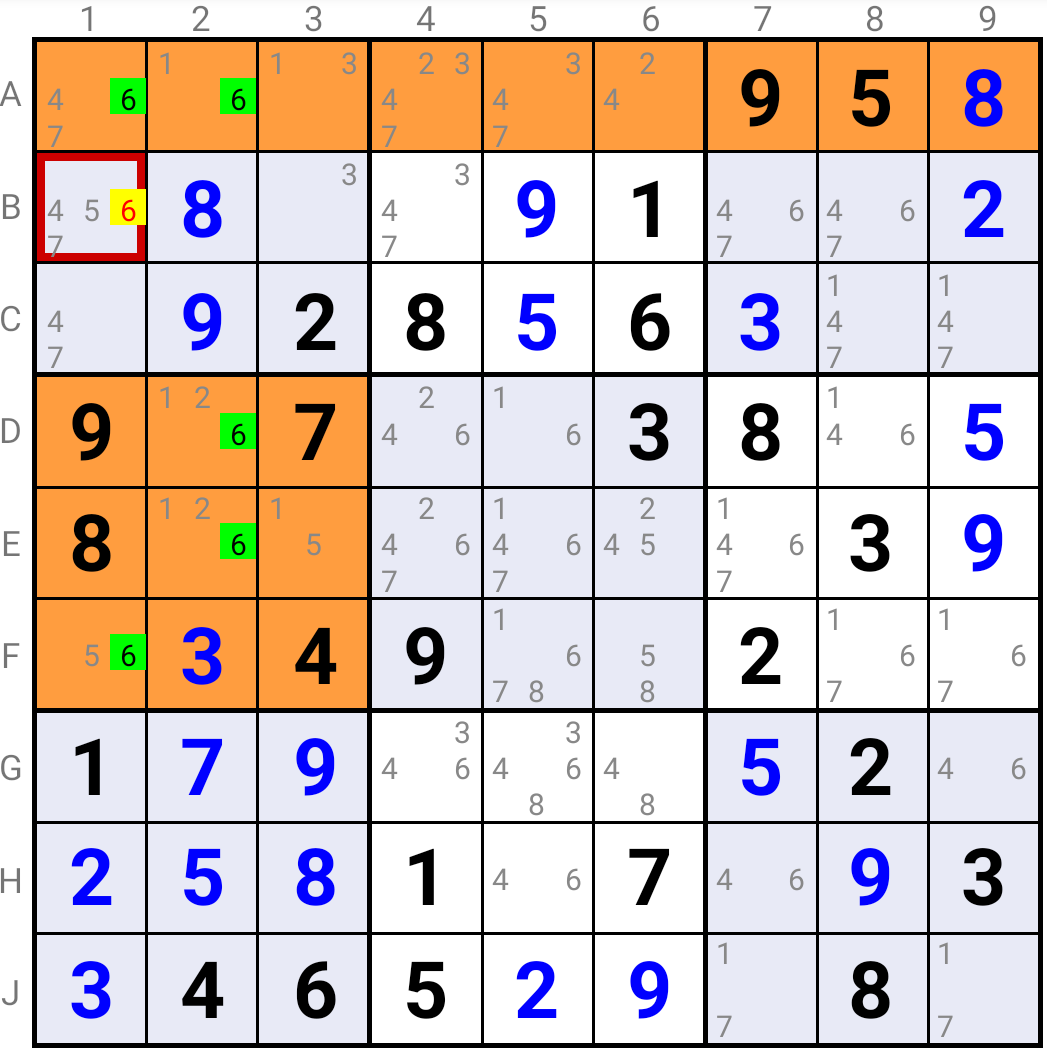
In the example above the Franken X-Wing is based on candidate 6 and it is made of Row "1" and Square "4".
If candidate 6 is the solution in A1, then it can not be the solution in B1.
If candidate 6 is the solution in A2, then it must be the solution in F1, which eliminates it from B1.
Whichever the solution for candidate 6 in Row "1", it can never be the solution in B2.

You can practice this strategy by installing the SudokuCoach application on your Android™ device.